贝叶斯法则
贝叶斯法则描述了P(h)、P(h|D)、P(D)、以及P(D|h)这四个概率之间的关系:

这个公式是贝叶斯方法论的基石。在数据挖掘中,我们通常会使用这个公式去判别不同事件之间的关系。
我们可以计算得到在某些条件下这位运动员是从事体操、马拉松、还是篮球项目的;也可以计算得到某些条件下这位客户是否会购买Sencha绿茶等。我们会通过计算不同事件的概率来得出结论。
比如说我们要决定是否给一位客户展示Sencha绿茶的广告,已知他所在的地区邮编是88005。我们有两个相反的假设:
- 这位用户会购买Sencha绿茶的概率,即:P(购买|88005);
- 不会购买的概率:P(┐购买|88005)。
假设我们计算得到P(购买|88005) = 0.6,而P(┐购买|88005) = 0.4,则可以认为用户会购买,从而显示相应的广告。
再比如我们要为一家销售电子产品的公司发送宣传邮件,共有笔记本、台式机、平板电脑三种产品。我们需要根据目标用户的类型来分别派送这三种宣传邮件。
比如我们有一位居住在88005地区的女士,她的女儿在读大学,并居住在家中,而且她还会参加瑜伽课程。那我应该派发哪种邮件呢?
让我们用D来表示这位客户的特征:
- 居住在88005地区
- 有一个正在读大学的女儿
- 练习瑜伽
因此我们需要计算以下三个概率:

并选择概率最大的结果。
再抽象一点,如果我们有h1, h2, ...hn等事件,它们就相当于不同的类别(篮球、体操、或是有没有患糖尿病等)。
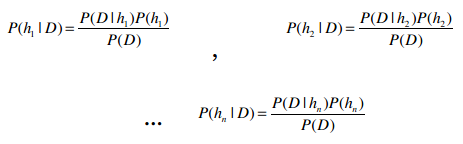
在计算出以上这些概率后,选取最大的结果,就能用作分类了。这种方法叫最大后验估计,记为hMAP。

我们可以用以下公式来表示最大后验估计:
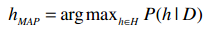
H表示所有的事件,所以h∈H表示“对于集合中的每一个事件”。整个公式的含义就是:对于集合中的每一个事件,计算出P(h|D)的值,并取最大的结果。
使用贝叶斯法则进行替换:

所以我们需要计算的就是以下这个部分:
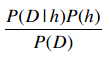
可以发现对于所有的事件,公式中的分母都是P(D),因此即便只计算P(D|h)P(h),也可以判断出最大的结果。那么这个公式就可以简化为:
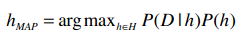
作为演示,我们选取Tom M. Mitchell《机器学习》中的例子。Tom是卡耐基梅隆大学机器学习部的首席,也是非常友好的一个人。
这个例子是通过一次血液检验来判断某人是否患有某种癌症。已知这种癌症在美国的感染率是0.8%。血液检验的结果有阳性和阴性两种,且存在准确性的问题:如果这个人患有癌症,则有98%的几率测出阳性;如果他没有癌症,会有97%的几率测出阴性。
我们来尝试将这些描述语言用公式来表示:
- 美国有0.8%的人患有这种癌症:P(癌症) = 0.008
- 99.2%的人没有患有这种癌症:P(┐癌症) = 0.992
- 对于患有癌症的人,他的血液检测结果返回阳性的概率是98%:P(阳性|癌症) = 0.98
- 对于患有癌症的人,检测结果返回阴性的概率是2%:P(阴性|癌症) = 0.02
- 对于没有癌症的人,返回阴性的概率是97%:P(阴性|┐癌症) = 0.97
- 对于没有癌症的人,返回阳性的概率是3%:P(阳性|┐癌症) = 0.03

Ann到医院做了血液检测,呈阳性。初看结果并不乐观,毕竟这种血液检测的准确率高达98%。那让我们用贝叶斯法则来计算看看:
- P(阳性|癌症)P(癌症) = 0.98 * 0.008 = 0.0078
- P(阳性|┐癌症)P(┐癌症) = 0.03 * 0.992 = 0.0298
分类的结果是她不会患有癌症。
如果想得到确切的概率,我们可以使用标准化的方法:

可以看到,血液检测为阳性的人患有这种癌症的概率是21%。

可能你会觉得这并不合情理,毕竟血液检测的准确率有98%,而结果却说Ann很可能并没有这种癌症。事实上,很多人都会有这样的 疑问。
我来说明一下为什么会是这样的结果。很多人只看到了血液检测的准确率是98%,但没有考虑到全美只有0.8%的人患有这种癌症。
假设我们给一个有着一百万人口的城市做血液检测,也就是说其中有8,000人患有癌症,992,000人没有。首先,对于那8,000个癌症病人,有7,840个人的血液检测结果会呈阳性,160人会呈阴性。
对于992,000人,有962,240人会呈阴性,30,000人呈阳性。将这些数字总结到下表中:
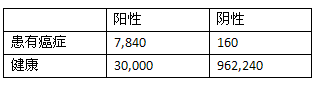
Ann的测试结果呈阳性,从上表看阳性中有30,000人其实是健康的,只有7,840人确实患有癌症,所以我们才会认为Ann很有可能是健康的。
还是没弄明白?没关系,在接触了更多练习后就会慢慢理解了。